Given this apparent electoral reality, many have wondered (including me) why President Obama’s administration would make a series of decisions that could lead to the appearance of bias against the Church that would potentially damage his support among some Catholics in an election year. Here is the widely-noted track record:
- In January 2012 the administration announced a new mandate requiring employers (and later their insurance companies; although many self-insure) to provide and fully pay for prescribed birth control, “morning after” pills, and medical sterilization for employees without a religious exemption that would include institutions such as Catholic universities, charities, or hospitals.
- The administration’s 2012 budget defunded the D.C. Opportunity Scholarship Program (for 2014 and beyond) that has provided tuition vouchers for many low income students who attend Catholic schools.
- In 2011, the administration defunded a Catholic Charities program that provided assistance to victims of human trafficking in finding food and shelter because it would not refer victims to providers of abortion and contraceptives.
- In a series of 2011 decisions the National Labor Relations Board (NLRB) ruled that some Catholic college campuses are not significantly religious to be exempt from labor rules. The NLRB argues that these campuses operate “as a secular educational institution.”
Why would an incumbent who needs the vote of Catholics to be re-elected create a record like this? Surprisingly, just looking at the polling data and the electoral math, President Obama doesn’t need to win the Catholic vote or the Protestant vote for that matter! How could this be? Quietly, another solid Democratic Party voting block has grown in size and importance in recent years that has a similar electoral effect to the Catholic-JFK vote. So much so that President Obama could lose both the Catholic and Protestant vote to the Republican nominee—even lose badly—and still win re-election. What the Catholic vote was to Kennedy, a new “None/Other vote” is to President Obama.
“Nones” are people without a religious affiliation (this does not mean they are all atheists or agnostics... they may even consider themselves to be religious or spiritual in some way—just not connected to any religious group). “Others” are a survey research catch-all category of people who have non-Christian religious affiliations. Twenty years ago the combined None/Other vote amounted to less than 10 percent of the population and the voting electorate. Today, the None/Other population percentage has risen to 22 percent (… and is expected to continue to grow in the future). This makes it nearly equivalent in size to the U.S. Catholic population percentage.
Democrats have not needed a majority of the Protestant vote (using the Exit Poll summary coding of “Protestant” which includes non-Catholic Christians) for quite some time and they have not had it either. In three recent national elections Democrats have obtained majorities of the Catholic vote (2002, 2006, and 2008) along with high percentages of the None/Other vote.
In 2012, a tipping point may have been reached. The None/Other vote is now sufficient in size and support for the Democratic Party where President Obama could lose the Catholic vote and still have a good chance of winning re-election. Why can’t Republicans just attempt to take some of the None/Other voters away from Democrats like any other portion of the electorate? It’s a bit of a zero-sum game and it all revolves around social issues on which None/Others generally disagree with Catholics and other Christians (as measured in the General Social Survey 2006-2010. I've aggregated to maximize the number of respondents and minimize margins of error for sub-groups).
For example, Nones and Others (defined in the figures below as religious, non-Christian) are significantly more likely than Catholics and other Christians to support abortion on demand. Just more than a third of Catholics and other Christians support this compared to about six in ten None/Others.
The None/Others are also largely supportive of same-sex marriage—registering support above 60%, whereas minorities of Catholics and other Christians agree with this proposition.
Only about a quarter of Catholics and other Christians strongly support government funding for embryonic stem cell research, whereas about half of None/Others do.
In a more general sense it is also the case that Christians are more conservative than non-Christians. Only 19% of Nones and 20% of those with non-Christian religious affiliations describe themselves as “slightly” to “strongly” conservative. A third of Catholics (33%) respond as such. The most conservative sub-group are other Christians of which 42% self-identify as a conservative.
Is there any common ground between these groups? If one moves away from political ideology and “culture war” issues and towards questions about government intervention to assist the poor or concern for the environment there are fewer differences. For example, about a three in ten of each group says they believe the federal government has a responsibility—more so than the individual or both the government and individuals—to improve the standard of living of all poor Americans.
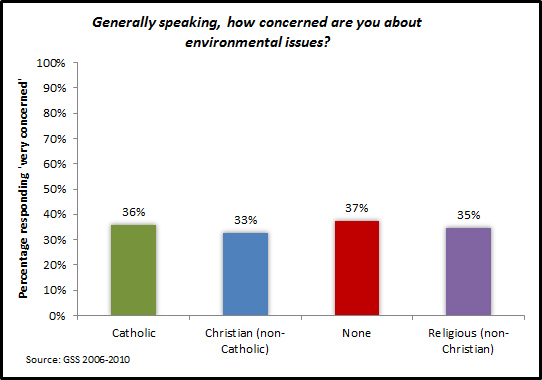
As shown in the figure below, very similar minority percentages in each group say they are “very concerned” about the environment. Despite President Obama's recent focus on this issue, I doubt “green energy” is going to have much traction among any segment of the electorate in this campaign. I do not have a recent survey data on gas prices to evaluate, but my hunch would be there would also not be much difference between the sub-groups on this issue either but I would expect that the level of concern for this would be significantly higher than concern for the environment.
The Republicans are only likely to draw some of the None/Other vote away from the Democrats in a magnitude that could alter electoral outcomes if one or more of the following occurred: 1) an economic downturn (...or $6 gas?), 2) a foreign policy failure by the president, or 3) a political scandal involving the president. But even with these events I’m not sure Republicans would ever have a chance of winning a majority of None/Other voters. The prevailing electoral tides are that strong.
In this sense Rep. Ron Paul may have been right when he said social conservatism is “a losing position” in the current electoral environment. There just may not be enough voters in the current electorate who are on the conservative side of “culture war” issues for this to be the focus of a winning Republican electoral strategy at the national/Electoral College level. There is some divide among Christians on these issues and a campaign focusing on these would likely drive None/Other in even greater numbers toward the Democrats.
I’ve run a variety of statistical simulations on the national popular vote as well as state popular votes using exit poll data (accounting for Electoral College votes). The “magic number” coming out of most of these for President Obama is 44. His support among Catholics and Protestants can go no lower than 44% and he will likely win re-election as long as his support among the None/Other vote is similar to what it has been in recent elections (typically above 70% overall). One of the reasons Democrats lost the majority popular vote for the House in 2010 was their extremely low support among Protestant voters. This dropped to 38% in 2010 from a 45% vote total for President Obama in 2008 (44% of Catholics voted for a Democrat in 2010 Congressional elections). If House Democrats would have attracted 44% of the Protestant vote in 2010, and all other outcomes remained the same, estimates for the national House vote would have increased to 50% Democratic overall.
In 2012, if Democratic “safe” states remain as such and President Obama is able to attract only 44% of the Protestant vote and 44% of the Catholic vote in each battleground state, he would likely narrowly lose Ohio and Iowa but still narrowly win majorities in Florida, Pennsylvania, Michigan, Wisconsin, Missouri, Nevada, and New Hampshire (in the latter two states one in four or more voters are expected to be None/Others). This would result in 291 Electoral College votes—a healthy surplus above the 270 needed to win re-election (for more on the math see this update).
In other words, perhaps we should not be so surprised to see President Obama take some of the positions he has in direct opposition to Catholic leaders. He may be risking majorities of the Catholic vote yet simultaneously he is also building more strength among None/Other voters. His campaign relies heavily on polling and research and I am sure they fully understand the implications of religious affiliation and vote preferences in the electorate. What seemed so irrational to some weeks ago is beginning to look to me like a campaign strategy. Don’t get me wrong, he cannot run the risk of seriously alienating Catholic or Protestant voters. He just has some room to maneuver given his likely strength among the None/Others. I don't think his campaign is really worried about “winning” the Catholic vote. In the 2012 political climate, getting just 44% would likely be a win.