According to physicist Stephen Hawking (a notable member of the Catholic Church’s Pontifical Academy of Sciences), we have to figure out how to leave this planet because in the next 1,000 or so years a mass extinction event (man-made or natural) will likely end human life.
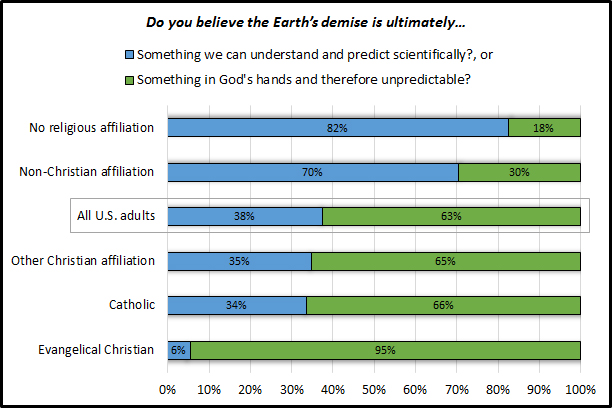
What happens when you ask people about the end of the world? CARA recently asked a national random sample of adults, “Do you believe the Earth’s demise is ultimately something we can understand and predict scientifically or something in God’s hands and therefore unpredictable?” More than six in ten believe it is in God’s hands. However, when you break that down by religious affiliation there is a big divide in opinion between Christians and those of other religious affiliations or no affiliation at all.
Only 6% of Evangelical Christians believe the Earth’s demise is something we can understand and predict scientifically. By comparison 34% of Catholics agree with this statement. At the other end of the spectrum, 82% of those without a religious affiliation (i.e., Nones) agree with the statement.
Barring divine intervention, it turns out there really are some things that are rather predictable about the possible “end of the world” in the long-term. The easiest is related to that brightest thing up in the sky we call the sun. Like any other star it has a lifespan and when it dies it will expand and take the Earth with it. The bad news is that, much earlier, in about 1 billion years it will be much hotter than it is now (regardless of any human activity) and Earth will no longer be a hospitable place for humans. With that in mind we asked Americans, “Scientists believe that in 4.5 billion years the Sun’s lifecycle will come to an end. Much earlier, in about 1 billion years, the sun will have become hotter and increased Earth’s temperature beyond a level where life, as we know it, is possible. Therefore, the long-term survival of humans may depend on space exploration and colonization. Do you believe that the destiny of human life is somewhere other than Earth or here on Earth?”
Hearing this reality, opinion is divided with 28% of adults saying human destiny is here on Earth and 27% saying this is to be found elsewhere in space. Most, 45% say they don’t know. Once again the opinion of Christians differ from others. Forty-one percent of Evangelicals believe the destiny of human life is on Earth compared to only 15% of those without a religious affiliation. Twenty-eight percent of Catholics say the destiny of human life is on Earth and 24% say it lies somewhere other than Earth (48% say they don’t know).
If Earth is doomed and human life can find a way to outlast it, then space is the place for the future. Seven in ten adults believe human exploration of space will be important (“very” or “somewhat”) in the future. Only one in ten say it is “not at all important.” Yet again, there are religious divides. Seventeen percent of Evangelicals believe space exploration to be “very” important compared to 41% of those without a religious affiliation. Thirty-six percent of Catholics believe it will be “very” important.
One might wonder why it matters if your religious affiliation is related to your views about the distant future, the ultimate demise of Earth, and space exploration. James Poulos, writing in Foreign Policy has argued, that Elon Musk, who has pledged to get humans to Mars soon, isn’t religious enough to colonize the red planet.
As you may have heard, Elon Musk (among others such as Neil DeGrasse Tyson, Richard Dawkins, and Bill Nye), believe that reality, as we know it, may be a computer simulation. As Musk notes, “There’s a one in billions chance we’re in base reality.” What is interesting is that many of these individuals are atheists or agnostics. They believe there is no God but also think it is possible or likely that everything we know is a simulation built by a creator? Am I the only one who finds this amusing? While some Christians may be the least inclined now to explore space, they could be the most able because they are also unlikely to believe reality is a complex video game and that reaching Mars would be an achievement rather than a pre-programmed outcome. Poulos writes, “Musk, and his Silicon Valley backers, are right that humanity’s destiny might be to extend life to other planets. But Musk’s seeming belief that we’re already stuck in a simulated world leaves only dubious reasons to endorse his understanding of what destiny means — and who ought to fulfill it.”
In the bleakness of space or the harsh environment of another planet, believing in a creator and an afterlife just might be what space explorers would need to be successful. On the other hand, as we have explored before, practicing religion in space will not be easy. “Do not go gentle into that good night...”
About the CARA Catholic Poll (CCP)
CARA partnered with GfK Custom Research (formerly Knowledge Networks) to conduct the survey. Interviews were conducted with 1,927 respondents between May 16 and May 26, 2016. The primary sample includes 1,010 self-identified Catholics (margin of error of ±3.1 percentage points). Additionally, 917 non-Catholics were interviewed. Of the non-Catholics, 311 are Evangelical Christians (margin of error of ±5.6 percentage points). Another 357 have some other Christian affiliation (margin of error of ±5.2 percentage points). A total of 76 had some other non-Christian affiliation (margin of error of ±11.2 percentage points) and 167 had no religious affiliation (margin of error of ±7.6 percentage points). Six respondents declined to state a religious affiliation. Statistical weights, created by GfK, are used to approximate the results for the U.S. adult population.